1. 히스토그램(Histogram)

1. 히스토그램(Histogram)    도수분포표에서 각 계급의 크기를 밑변, 도수를 높이로 하여 만들어진 직사각형의 그래프를 히스토그램이라고 한다.   가.  막대그래프와 히스토그램    계급의 크기가 없을 때 막대로 띄엄띄엄 나타낸 그래프가 막대그래프이다.    막대그래프는 막대의 길이가 도수를 나타내고, 히스토그램은 직사각형의 높이가 도수를 나타낸다.   따라서, 막대그래프는 흩어져 있는 이산변량을 나타내는 데 편리하고, 히스토그램은 연속변량을  나타내는 데 편리하다.

2. 도수분포다각형     히스토그램에서 각 직사각형의 윗변의 중점을 차례로 선분으로 연결하고 , 양 끝은 도수가 0인 계급을 하나씩 추가하여 연결한 그래프를 도수분포다각형이라고 한다.

1.  히스토그램의 직사각형의 넓이의 합과 도수분포다각형으로 둘러싸인 부분의 넓이는 서로 같다.

 

----------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------

문제에서는 히스토그램의 직사각형의 넓이 = 도수분포다각형과 가로축으로 둘러싸인 부분의 넓이

임을 설명하여라 라고 하였습니다.

 

1. 히스토그램의 직사각형의 넓이.

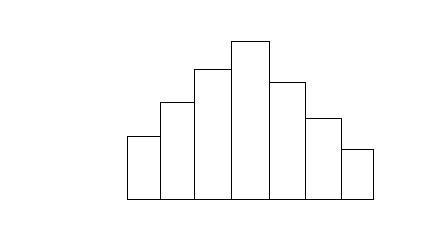
계급의 구간을 일정하게 설정하고 히스토그램을 그리면

 

와 같이 됩니다.

 

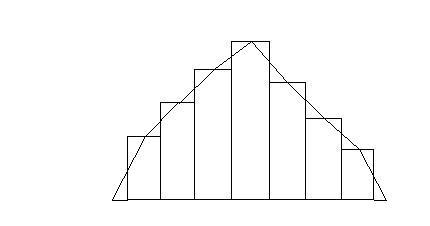
2. 히스토그램에다 도수분포다각형을 그리면

 

와 같이 됩니다.

 

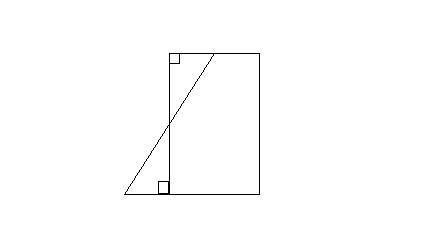
여기서 가장 왼쪽 부분을 확대하면

 

와 같이 되고, 도수분포다각형의 선에 의해 직각 삼각형 2개가 생깁니다. 이 2개의 삼각형은 합동임을 알 수 있습니다. 여기서 도수분포다각형 선위의 삼각형을 잘라서 왼쪽 아래 삼각형부분으로 옮겨 놓습니다.

 

이런식으로 계속 도수분포다각형위 생기는 삼각형을 잘라서 도수분포다각형 선 아래 빈공간에 옮겨 놓으면, 처음 히스토그램의 사각형면적은 모두 도수분포다각형 선아래와 가로축에 의해 생기는 면적을 다 채우게 됩니다.

 

따라서 히스토그램의 직사각형의 넓이 = 도수분포다각형과 가로축으로 둘러싸인 부분의 넓이 가 됩니다.

 

 -------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------

히스토그램과 도수분포다각형 히스토그램 도수분포표의 계급을 가로로 하고 도수를 세로로 하여 직사각형을 그린 그래프. 직사각형의 넓이는 도수에 비례한다. 도수분포다각형 히스토그램의 각 직사각형의 중점을 차례로 선분으로 연결하여 만든 다각형. 특히 양 끝점은 도수가 0인 계급이 하나씩 있는 것으로 생각하여 그 중점을 잡은 것이다.  히스토그램(histogram) 도수분포다각형 (frequency distribution polygon) 도수분포표 계급(몸무게) 도수(학생수) 25이상~30미만 30   ~  35 35   ~  40 40   ~  45 45   ~  50 50   ~  55 55   ~  60 60   ~  65 1 3 5 6 3 4 2 1 합 계 25명 　 용어사전으로

Update : 1999년 12월 29일  수학선생님®  수학교육연구©   mathel@unitel.co.kr